Reverse
Preliminary
I’m an absolute beginner at reverse engineering CTFs, either because I don’t have the motivation to chew through the extensive world of decompilers and Assembly and dynamic analysis and whatnot or because I’m really lazy to do a ton of code analysis.
es3n1n arguably wrote the most beautiful challenges of the entire contest this time around. Aside from other really, really good web challenges, this category actually has the reverse spirit all around.
Though, unfortunately I could only solve one myself. One has a bug (is that even a bug?), the other is probably one of the hardest technical reverse challenges for a two-day long contest with only 8 solves after the contest ends.
The Challenges
rev/bleh
- Author
- es3n1n
- Category
-
rev - Files
- rev_bleh.tar.gz
- Flag
-
osu{bl3h_bleh_b13h_m4n_1_l0v3_aut0_r3vs_e4fb25f} - Solved in time?
-
yes
bleh :p
Even though I said I solved this in time, I never ended up submitting in time just because I woke up a few hours after the contest announced its ending. I fell asleep when the solve script I wrote was doing its thing.
Another thing: there might be multiple ways to solve this challenge. In my findings I’ve found two ways, one that uses, to a certain degree, math, the other brute-forces the solve. The mathematical solve will be mentioned later.
Upon downloading the challenge file and extracting it, we can see there are… 3,842 files, bleh0...bleh3841, lol. That’s an incredible sight.
Opening some of these reveals that they do the same thing… there’s just one problem. Something about them was different.
I used Ghidra to do this. Any other tool, for example BinaryNinja or IDA, probably produces the same result, maybe with differences in its pseudo-code or naming conventions.
Most inspections should be self-explanatory:
- The first 32 bytes of the string used to compare to the key is a static key,
PL4YING_CTFS_ISNTBETTER_THAN_OSU - The other 32 bytes are for our input
- For each
i,
b = FUN_00101337(input[i], key[i], state)state = (uint)bout[i] = b- Then, the output of that has to match the hardcoded target:
strncmp(out, target, 0x20) == 0We need to find an input such that the transformed out bytes matches what’s in the obfuscated target array.
The main logic is in FUN_00101337, as denoted, so we check there:
local_c4 = FUN_001011c9(param_1, 6);local_d4 = FUN_001011c9(param_2, 0x80);local_e4 = FUN_00101280(param_3, 0x80);
local_78 = local_98 ^ local_a8; // local_98 = local_d4, local_a8 = local_c4local_68 = local_e4 + (int)local_78;return local_68;That’s basically doing
out = FUN_00101280(state, 0x80) + (FUN_001011c9(key, 0x80) ^ FUN_001011c9(input, 6))FUN_001011c9(uint x, int n) is doing basically x + n, since it’s just recursive with a constant depth param_2. FUN_00101280 (uint x, int n) is doing basically x - n for the same reason as well, so we can simplify out as follows:
out = (state - 128) + ((key + 128) ^ (input + 6))This is the state we want to begin solving the challenge.
Let’s just solve bleh0 first initially, then check the other bleh files to see what these files differ. Then we can repeat the solve for all the other ones.
The (likely) intended solve
For a CTF contest, normally we want to solve the challenges as quickly as possible.
After the transforms, we end up with:
out = (state - 128) + ((key + 128) ^ (input + 6))Notice that only the low 8 bits of out are used both for the output byte comparison and as the next state. So all arithmetic can be done modulo 256.
Given:
T = targetS = state (low 8 bits)K = keyI = input (unknown)We rewrite out:
T = (S - 128) + ((K + 128) ^ (I + 6)) (mod 256)Brute-forcing this is cheap, since we observed at each i, our executable checks one output byte T[i] produced from three things: the known key byte K (which is key[i]), the state S with an initial low byte of 0x1337 & 0xff, and the unknown I. We can just check all 256 possible Is and see which one produces T[i]. There is exactly one candidate for every byte, so worst case scenario we only have to do 8192 = 256 * 32 transform evals.
This is easily implemented in Python:
def fa(x, n): # this is FUN_001011c9 return (x + n) & 0xffffffff
def fb(x, n): # this is FUN_00101280 return (x - n) & 0xffffffff
def transf(i, k, s): # simulate FUN_00101337, observe that caller uses low byte of return return (fb(s, 128) + (fa(k, 128) ^ fa(i, 6))) & 0xffffffff
def main(): key = b"PL4YING_CTFS_ISNTBETTER_THAN_OSU" # target bytes from disasm t_signed = [ 0x73, -0x6d, -0xf, 0x58, 0x7d, -0x61, -0x35, 0x34, -0x57, 0x0b, 0x7c, -0x1f, 0x46, 0x74, -0x23, 0x4f, -0x43, 0x3a, -0x47, 0x21, -0x7d, -10, 0x5a, -0x3e, 0x24, -0x5d, 0x1a, -0x6d, -4, 0x75, -0x1c, 0x47 ] target = [(x + 256) % 256 for x in t_signed]
s = 0x1337 & 0xff f = []
for i in range(32): t = target[i] k = key[i] cand = None for c in range(256): o = transf(c, k, s) & 0xff if o == t: cand = c break if cand is None: raise RuntimeError(f"no cand for i={i}") f.append(cand) s = t # next state becomes the output byte (low 8 bits)
out = "".join(f"{b:02x}" for b in f) print("brute'd hex:", out) print("raw bytes:", bytes(f))
if __name__ == "__main__": main()Sample run succeeds:
brute'd hex: 6666643866666530303031303461343634393436303030313031303130303630raw bytes: b'ffd8ffe000104a464946000101010060'Pass the raw bytes to the executable:
$ ./bleh0ffd8ffe000104a464946000101010060Nicely doneOf course, this approach has caveats. I’ve only tried this after doing the challenge by some maths, this is the simplest form of this method I’ve came up with.
The practical solve
I had time, and I was soloing this CTF as a first-timer so I was willing to sit there and do this. I’m not sure if this or the brute-force was the intended solve, but oh well.
Throwback to our out:
out = (state - 128) + ((key + 128) ^ (input + 6))About the low 8 bits, we can observe that caller stores b into a byte array and sets state = (uint)b. That means only the low 8 bits of out matter for both the output byte comparison and the next state’s value. As follows, we can do all math modulo 256.
Again, given:
T = targetS = state (low 8 bits)K = keyI = input (unknown)We rewrite out:
T = (S - 128) + ((K + 128) ^ (I + 6)) (mod 256)We’re solving for I, so let’s rearrange:
Z = T - (S - 128) (mod 256), with Z = (K + 128) ^ (I + 6)
I = ((K + 128) ^ Z) - 6 (mod 256)With that, for each byte i we:
- From
TandS, findR - Compute
I = ((K + 128) ^ Z) - 6(mod 256) - Set
S = T, then continue.
Every I is deterministic since we know the key and target. Let’s try the first byte.
S = 0x37K = 0x50T = 0x73
R = T - (S - 128) (mod 256) = 0xBC
I + 6 = (K + 128) ^ RK + 128 = 0xD0(K + 128) ^ R = 0x6C
I = 0x6C - 6 = 0x660x66 is f in ASCII. If you do this across all bytes you get the full input hex, but let’s not do this by hand. Implementing this in Python is way simpler:
key = b"PL4YING_CTFS_ISNTBETTER_THAN_OSU"
t_signed = [ 0x73, -0x6d, -0xf, 0x58, 0x7d, -0x61, -0x35, 0x34, -0x57, 0x0b, 0x7c, -0x1f, 0x46, 0x74, -0x23, 0x4f, -0x43, 0x3a, -0x47, 0x21, -0x7d, -10, 0x5a, -0x3e, 0x24, -0x5d, 0x1a, -0x6d, -4, 0x75, -0x1c, 0x47]
# convert signed entries to 0..255 bytestarget = bytes([(x + 256) % 256 for x in t_signed])
def byte_mod(x): return x & 0xff
S = 0x1337 & 0xfff = []
for i in range(32): T = target[i] K = key[i] # R = T - (S - 128) (mod 256) R = byte_mod(T - (S - 128)) I = byte_mod(((K + 128) ^ R) - 6) f.append(I) S = T
# resultsout = "".join(f"{b:02x}" for b in f)print("hex:", out)print("raw bytes:", bytes(f))We get the same thing as brute'd on bleh0:
hex: 6666643866666530303031303461343634393436303030313031303130303630raw bytes: b'ffd8ffe000104a464946000101010060'Coincidentally that’s also the start of a JPEG/JFIF header, seeing 4a464946. From that, we can infer the other 3,841 files probably are parts of the big picture. They do the same thing, just with a different obfuscated target array.
Do the same thing for those files (and probably don’t do this manually, lol), concatenate and decode as hex just as the flag intended, you’ll find the image. A funny image at that.

There’s the flag. This challenge is solved.
rev/tosu-1
- Author
- es3n1n
- Category
-
rev - Files
- rev_tosu-1.tar.gz
- Flag
-
osu{cl1ck_7h3_c1rcl35_w1th_n0_b34t} - Solved in time?
-
no
Welcome to the first part of the series of tosu challenges.
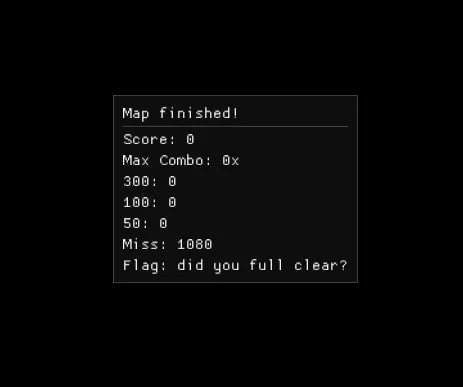
Full clear the attached map scoring only 300s.
From bleh :p to this. Amazing stuff, difficulty 3/5.
This challenge is mainly just observe and think, not much coding is involved. Most of the solving process outlined here is actually just my thinking process, there’s literally no math in here, so I’ll not show a lot of decomp. code.
Now, the solve for this challenge is incredibly funny, and the inspection process is also amazingly peak content. Upon opening the challenge archive, we can see a Windows executable file tosu.exe and a map file chal1.map.
Run tosu.exe in CLI, supply the map as an argument. Lo and behold, impossible osu! gameplay.
Initially what comes to mind before one begins to solve this challenge is either:
- Do something to full clear the map, as in, full 300 it, whatever means possible,
- Or just patch the executable to ignore the hit results.
Upon inspections, we can see the challenge works by having a hasher that gets updated throughout the process of us sitting there and watch the circles appear and disappear (ultimate yap), and it works like this:
- On challenge start: The hash is updated using all objects and difficulty settings.
- On any hit or miss action: The hash is updated using that hit result and the object index (there might be something else, but we don’t care)
- On challenge end: The hash is updated using whatever stats will be shown on the screen and all the objects once again.
That hash is then used to decrypt the flag. The obvious solution that comes to mind to get the correct hash, as per the description of this challenge, is to full clear the map. Somehow.
But, being one lucky person who went to rev only after es3n1n updated the description of the challenge, adding this ONE line:
If your solver isn't working and you're confident that it seems correct but still can't get the flag, try achieving the perfect score with no reflection of it in the GUI. Essentially, you should have a perfect score without ever touching the circles, and the counts on the final screen should all be zero except the miss count, which should be 1080. (It will make sense if you're stuck in that place)Then just make a miss count as 300 internally so it gets added to the hasher, right?
Yes.
Tracing the function where hit judgements are counted and added to the hasher, this is where the miss is counted:
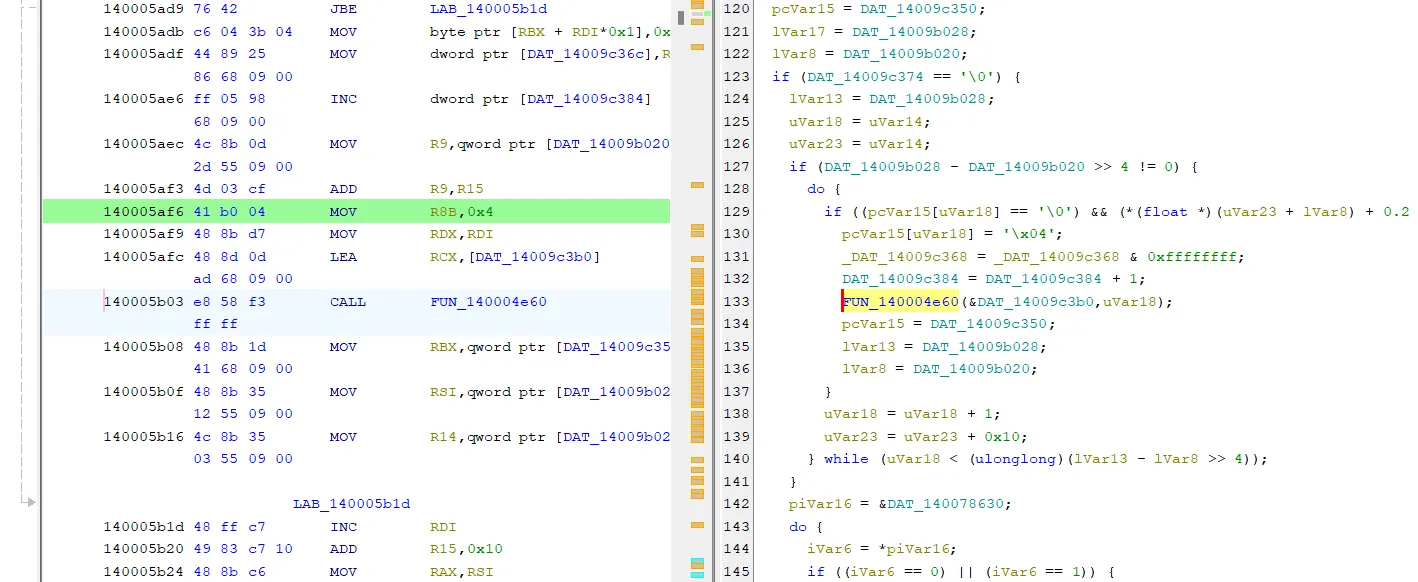
I think if you analyzed this on runtime with a couple tools, you’d have a much easier time finding that out. I had time after the Sunday tournament game, so there it is.
Anyway, miss is 0x4. Patch that to 0x3, the challenge is solved…
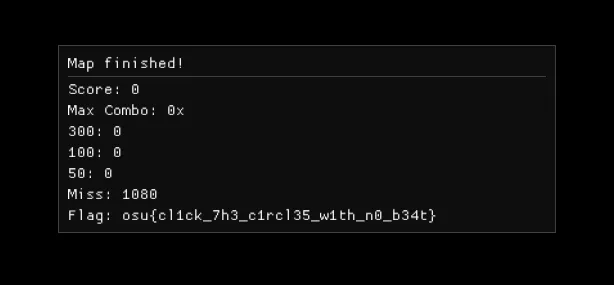
Post-contest, many people in different teams confessed they initially tried to make an aimbot that literally just annihilates this game, in one way or another, just to end up solving this challenge a single minute after the description edit. The description, to be fair, was misleading as hell. I’d have done the same thing if I wasn’t lucky.
One experience I got from this was to stop thinking of annihilating the impossible. Thanks, es3n1n.
rev/tosu-2
- Author
- es3n1n
- Categories
-
rev crypto - Files
- rev_tosu-2.tar.gz
- Flag
-
osu{e5ed275c44694a8f9688065ff540e1057dfbc948} - Solved in time?
-
no
(˶˃ ᵕ ˂˶) .ᐟ.ᐟ
As I mentioned, by the time the contest ends, there are 8 solves on this challenge. I was away for the entire Sunday in my timezone, since I had a tournament game to play. There’s no way I would look into this challenge…
But one thing es3n1n added when I came back to check the #reverse channel:

Yeah… no. However, a CTF team, who finished this contest at second place, has a quite detailed and nice write-up of how they solved this challenge. Give that a read, learn from the best!
Here goes: https://slight-smile.com/writeups/osu-ctf-25/#rev—tosu-2
